MA.5.4 反常积分

• 反常积分: 不满足上述两条件之一的积分
  • 包含无穷区间上的积分和瑕积分 (被积函数无界)
• 相对于反常积分而言, 定积分称为常义积分

反常积分

一、无穷区间上的积分

Solution

$$\begin{array}{rl}dW& =\frac{GMm}{x^2}dx\\ W& =G{M}_m{\int }_R^{R+H}\frac{1}{x^2}dx\\ & =GMm(\frac{1}{R}-\frac{1}{R+H})\dots GM=g{R}^2\end{array}$$

• 若 $H\to \mathrm{\infty }$ : $W=mgR$
• 动能转换 : $v_0=\sqrt{2gR}=11.2\text{ km/h}$ 第二宇宙速度

Solution

实际上是无穷的，所以是瑕积分

无穷积分

无穷积分的敛散性判断

• 若

则称 ${\displaystyle {\int }_a^{+\mathrm{\infty }}f(x)\mathrm{d}x}$ 收敛, 且其值为

• 若上述极限不存在, 则称 ${\displaystyle {\int }_a^{+\mathrm{\infty }}f(x)\mathrm{d}x}$ 发散.

结论: 无穷积分的敛散性是通过 F(变上限积分) 的敛散性定义的

类似可定义 ${\displaystyle {\int }_{-\mathrm{\infty }}^{b}f(x)\mathrm{d}x=:\underset{B\to -\mathrm{\infty }}{lim}{\int }_B^{b}f(x)\mathrm{d}x}$ 的收敛与发散.

实际上，$a-\mathrm{\infty },c-\mathrm{\infty }$的积分是等价（同敛散性）的，只差一个 $a$ ~ $c$ 的积分：

${\int }_a^{+\mathrm{\infty }}={\int }_a^c+{\int }_c^{+\mathrm{\infty }}$ (同理可互换$a,c$)

更一般的，${\int }_{-\mathrm{\infty }}c+{\int }_c^a+{\int }_a^{+\mathrm{\infty }}={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}$ (定理1)

定理: 同敛散性

定理: 广义 N-L 公式

例题

Solution

$\begin{array}{rl}{\int }_1^{+\mathrm{\infty }}\frac{dx}{x^{\alpha }}& =\{\begin{array}{ll}{\frac{x^{1-\alpha }}{1-\alpha }|}_1^{+\mathrm{\infty }},& (\alpha \ne 1)\\ {\ln x|}_1^{+\mathrm{\infty }},& (\alpha =1)\end{array}\\ & =\{\begin{array}{ll}\frac{1}{\alpha -1},& \alpha >1\\ +\mathrm{\infty },& \alpha \le 1\end{array}\end{array}$

结论: 当且仅当 $\alpha >1$ 的时候收敛

Solution

由于 ${\int }_0^{+\mathrm{\infty }}\frac{x}{1+x^2}dx={\frac{1}{2}\ln (1+x^2)|}_0^{+\mathrm{\infty }}=+\mathrm{\infty }$ 故原积分发散

神奇小号

神奇小号: 曲线 $y=1/x$

$(x\ge 1)$ 绕 $x$ 轴旋转曲面.

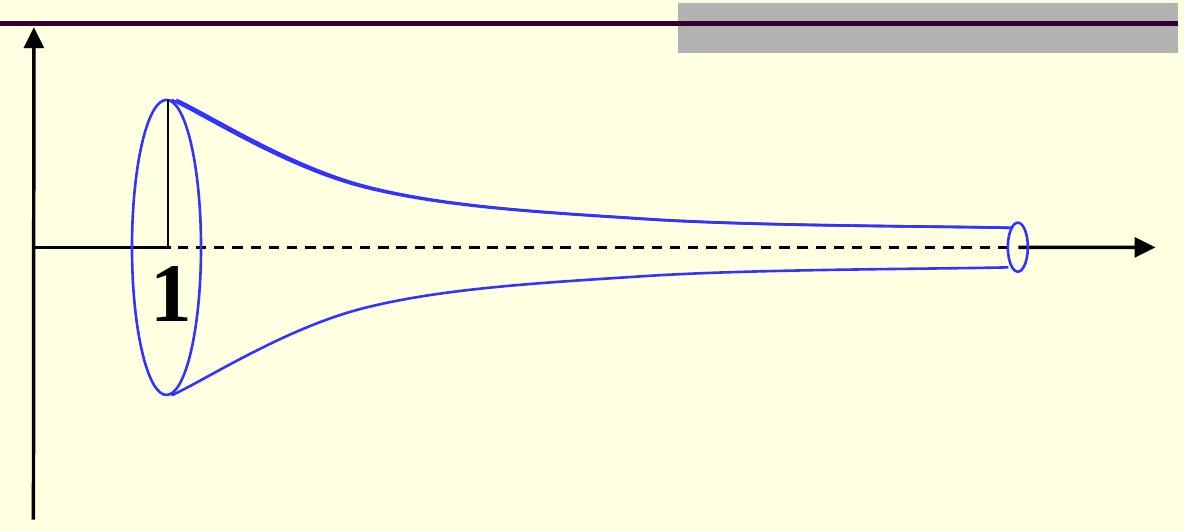
托里拆利(Torricelli)小号

小号特点

表面积

而 $\frac{1}{x}$已经趋近于正无穷，根号内始终大于一，所以为正无穷

所围体积

$V=\pi {\int }_1^{+\mathrm{\infty }}\frac{1}{x^2}\mathrm{d}x=\pi$

参见上例题的 $\alpha =2$ 的特殊情况

二、瑕积分

• #瑕点 ：$f$ 在 $b$ 任意一个去心领域都无界
• 此处借用了定积分的符号，并不是定积分

瑕积分的敛散性

• 若

则称 ${\int }_a^{b}f(x)\mathrm{d}x$ 收敛, 其值定义为

• 此时积分符号有两种含义：数值 $I$；瑕积分

• 若上述极限不存在, 则称 ${\int }_a^{b}f(x)\mathrm{d}x$ 发散.

• 当 $a$ 为 $f$ 的瑕点, 定义 ${\int }_a^{b}f(x)\mathrm{d}x=:\underset{\epsilon \to 0^{+}}{lim}{\int }_{a+\epsilon }^{b}f(x)\mathrm{d}x$

• 当 $c\in (a,b)$ 为 $f$ 的瑕点, 定义

当且仅当右端 同时独立收敛 时（上限 $c^{-}$ ,下限 $c^{+}$）, 称 左端收敛 .

定理: N-L 公式

例题

Solution

$x=0$ 为瑕点

$${\int }_0^1\frac{1}{x^{\alpha }}dx=\{\begin{array}{l}{\frac{x^{1-\alpha }}{1-\alpha }|}_0^1,\alpha \ne 1\\ {\ln x|}_0^1,\alpha =1\end{array}=\{\begin{array}{l}\frac{1}{1-\alpha },\alpha <1\\ +\mathrm{\infty },\alpha ⩾1\end{array}$$

故原积分当且仅当 $\alpha <1$ 时收敛

Solution

发散

$x=0$为瑕点

注意同时独立，若所得为0，其实是默认了 $a=b$

三、反常积分的换元和分部积分

换元法

• 外形与定积分的换元法无区别，但是 $\beta$ 可能也是瑕点，带不进去=>使用极限
• 若换元后 $\beta$ 不再是瑕点，则变成定积分，且原积分收敛
• $\beta$ 也可能为无穷：无穷积分

分部积分

• 同上，瑕点处理解成取极限

例题

Tips

无穷积分、三角代换

Solution

$$\begin{array}{rlr}\begin{array}{rl}& \stackrel{x=\tan t}{=}{\int }_0^{\pi /2}\frac{{\sec }^{2}tdt}{(1+{\tan }^{2}t)(1+{\tan }^{\alpha }t)}\\ & ={\int }_0^{\pi /2}\frac{{\cos }^{\alpha }t}{{\cos }^{\alpha }t+{\sin }^{\alpha }t}dt\\ & \stackrel{\text{ 三角替换 }}{=}{\int }_0^{\pi /2}\frac{{\sin }^{\alpha }t}{{\sin }^{\alpha }t+{\cos }^{\alpha }t}dt\\ & =\frac{1}{2}({\int }_0^{\pi /2}\frac{{\cos }^{\alpha }t}{{\cos }^{\alpha }t+{\sin }^{\alpha }t}dt+{\int }_0^{\pi /2}\frac{{\sin }^{\alpha }t}{{\sin }^{\alpha }t+{\cos }^{\alpha }t}dt)\\ & =\frac{1}{2}\left({\int }_0^{\pi /2}1dt\right)\\ & =\frac{\pi }{4}\end{array}& & \end{array}$$

$0$ 不再是瑕点

Solution

$$\begin{array}{rlr}\begin{array}{rl}{\int }_0^1\ln xdx& ={x\ln x|}_0^1-{\int }_0^{1}x\frac{1}{x}dx\\ & =(0-0)-{x|}_0^1\\ & =-1\end{array}& & \end{array}$$

$0$ 不再是瑕点

Proof

$x=0$ 是瑕点

$$\begin{array}{rlr}\begin{array}{rl}& {\int }_0^{\pi /2}\ln \sin xdx\\ & ={x\ln \sin x|}_0^{\pi /2}-{\int }_0^{\pi /2}x\frac{\cos x}{\sin x}dx\\ & \text{ 其中: }\underset{x\to 0^{+}}{lim}\frac{\ln \sin x}{\frac{1}{x}}\stackrel{\left(\frac{\mathrm{\infty }}{\mathrm{\infty }}\right)}{=}\frac{\frac{\cos x}{\sin x}}{-\frac{1}{x^2}}=-\underset{x\to 0^{+}}{lim}\frac{x^2\sin x}{\cos x}=0\end{array}& & \end{array}$$

由于 ${\int }_0^{\pi /2}\frac{x\cos x}{\sin x}dx$ 为定积分，故 ${\int }_0^{\pi /2}\ln \sin xdx=-{\int }_0^{\pi /2}x\frac{\cos x}{x}dx$ 从而收敛

---

Solution

上式容易判断敛散性，但并不容易计算值

$$\begin{array}{rlr}\begin{array}{rl}I& ={\int }_0^{\pi /2}\ln \cos xdx\\ & =\frac{1}{2}{\int }_0^{\pi /2}(\ln \sin x+\ln \cos x)dx\\ & =\frac{1}{2}{\int }_0^{\pi /2}\ln (\sin x\cos x)dx\\ & =\frac{1}{2}{\int }_0^{\pi /2}(\ln \frac{1}{2}+\ln \sin 2x)dx\\ & =-\frac{\ln 2}{4}\pi +\frac{1}{2}{\int }_0^{\pi /2}\ln \sin 2xdx\end{array}& & \end{array}$$

由于

$$\begin{array}{rlr}\begin{array}{rl}& {\int }_0^{\pi /2}\ln \sin 2xdx\\ & \stackrel{2x=t}{=}\frac{1}{2}{\int }_0^{\pi }\ln \sin tdt\\ & ={\int }_0^{\pi /2}\ln \sin tdt\\ & =I\end{array}& & \end{array}$$

由前式: $I=-{\displaystyle \frac{\ln x}{2}}x$